Coprime numbers are numbers that have no common factors other than 1. When working with coprime numbers, it’s often helpful to think of them as having no factors in common rather than thinking of them as numbers that have a certain number of factors in common. The difference may seem subtle, but it can often help you avoid committing the cardinal sin of checking your answer when you’ve got the right answer.
For example, 41 is a coprime number with 9 since the only common factor of 41 and 9 is 1. One of the best examples of a coprime number is 11 and 13 which has 1 as its only common factor. In the case of 4 and 9, even though 4 and 9 form a pair of co-prime numbers, 4 is considered a composite number since it has 1, 2, and 4 as its factors. On the other hand, 9 is a composite number since it has 3 factors, one being 1 and the other two being 3 and 9. Thus, 4 and 9 are coprime numbers since they have 1 as their only common factor.
How to Find Coprime Numbers?
Coprime numbers can be tricky to work with, especially when it comes to finding the greatest common factor (GCF) of two or more coprime numbers. Fortunately, there are a few simple rules you can follow to help you find the GCF of two or more coprime numbers.
- Start by listing all the factors of your numbers.
- As long as they’re coprime, the factors you will have 1 as the only common factor.
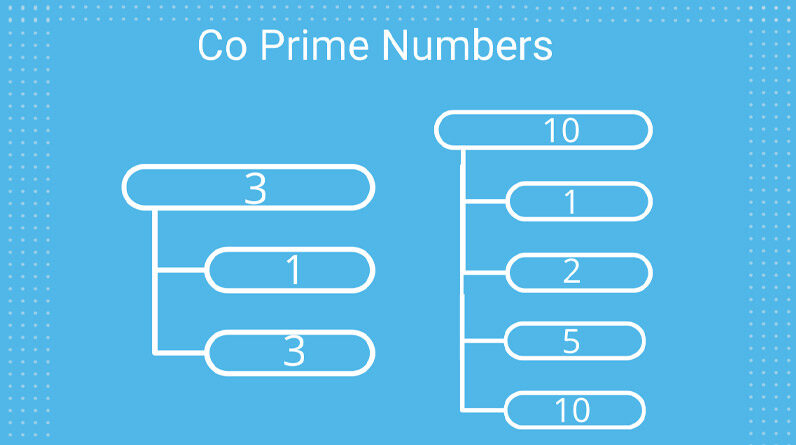
- For example, take 4 and 9. Factors of 4 are 1, 2, and 4 itself while factors of 9 are 1, 3, and 9. Thus, it can be seen that 4 and 9 are coprime numbers as they have 1 as their only common factor.
Properties of Coprime Numbers
Coprime numbers share some common properties. Some of the properties of coprime numbers are as follows.
- The sum of any coprime numbers is always coprime to the product of any other coprime numbers. For example, 4 and 9 are coprime numbers. The Sum of 4 and 9 is 13. The product of 4 and 9 is 36. Next, the factors of 13 are 1 and 13 while the factors of 36 are 1, 2, 3, 4, 6, 9, 12, 36. Thus, it can be seen that 13 and 36 are coprime numbers with 1 as their only common factor.
- Coprime numbers have 1 as their HCF always. For example, the HCF of 4 and 9 is 1.
- The product of two coprime numbers gives the LCM of the two numbers. For example, the LCM of 4 and 9 can be calculated just by multiplying the two numbers i.e. LCM(4,9) is 36.
- As even numbers have 2 as their common factor in all the cases, making them non-coprime or even numbers can never be coprime numbers.
- Prime numbers are always coprime. This is because prime numbers have 1 as the only common factor making them coprime numbers. For example, 11 and 13 are prime numbers with factors of 11 as 1 and 11, factors of 13 as 1 and 13. Thus, 11 and 13 are coprime numbers as they have 1 as their only common factor.
Conclusion
It’s fascinating to think about all of the different ways that coprime numbers are used in our daily lives. In math and science, coprime numbers provide an excellent way to prove theorems and make predictions about the world around us. In other fields, coprime numbers can be used to create software and systems that help us to make smarter decisions and to improve the lives of others. For more information on coprime numbers visit Cuemath. They are the best source to learn some complex concepts of mathematics more simply.